مبانی هندسه

بعد از حدود دو هزار سال از مطرح شدن امکان تثلیث زاویه، تربیع مربع و تضعیف مکعب فقط به کمک خط‌کش نامدرج و پرگار،بالاخره در قرن هجدهم میلادی ثابت شد که به کمک خط‌کش نامدرج و پرگار نمی‌توان این مسائل را حل نمود و حتی مسئله در حالات کلی‌تری حل شد.

مثلاً به عنوان یک نتیجه از آن اثبات، می‌دانیم که نمی‌توان یک هفت‌ضلعی منتظم را فقط با استفاده از قوانین کلاسیک یونانیان  (یعنی فقط با خط‌کش نامدرج و پرگار) رسم کرد.

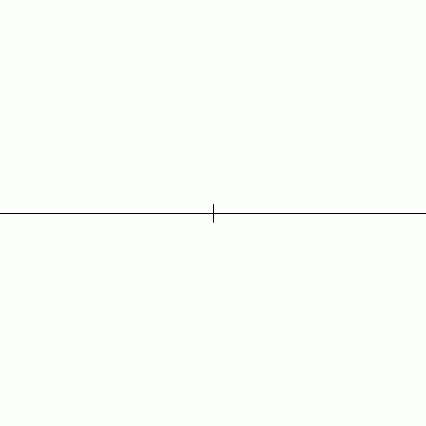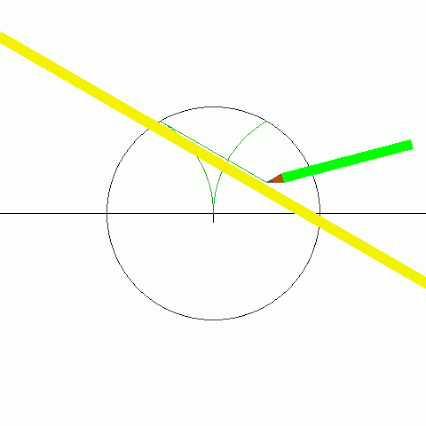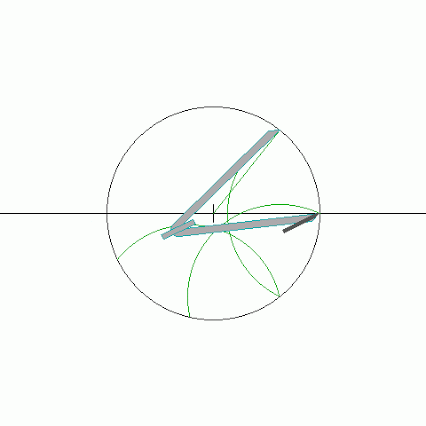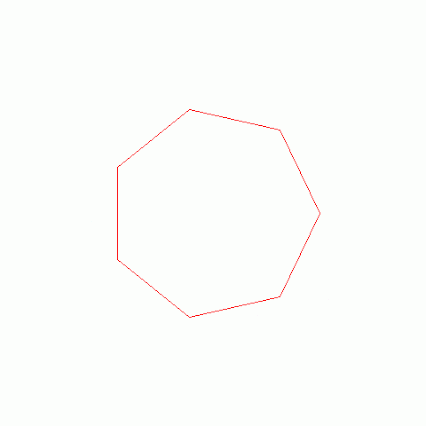
اما در طول تاریخ ترسیم مرزی (Neusis Construction) مرسوم شد که در آن، استفاده از یک خط‌کش با دو نشانه بر آن مجاز است و بدین طریق می‌توان طول را انتقال داد.

در شکل زیر نحوه‌ی ترسیم مرزی هفت‌ضلعی منتظم را مشاهده نمایید. 

البته در حین انجام ترسیم مرزی زیر،‌ تلاش کنید مرحله یا مراحلی که از قوانین کلاسیک یونان در ترسیم تخطی شده است را مشخص نمایید. 

در مقاله زیر با ترسیم‌های هندسی با قوانین کلاسیک یونان باستان (فقط  به کمک خط‌کش نامدرج و پرگار)  و سرانجام آنها آشنا می‌شوید:

مسائل سه‌گانه ترسیم در یونان باستان

در فایل زیر که برگرفته از کتاب‌‌های نشر الگو است، می‌توان ترسیم‌های مقدماتی و جالبی را مشاهده نمود. همچنین در پایان آن تمرین و تست نیز از این موضوعات وجود دارد

ترسیم‌های هندسی مقدماتی - نشر الگو

در مقاله زیر به طور کلی درباره ترسیم‌های هندسی در  دوره‌های مختلف سخن گفته شده است.

ترسیم‌های هندسی
(با تشکر از دکتر عرفان صلواتی)

درباره  چندضلعی‌های ترسیم‌پذیر با قوانین کلاسیک یونان و تاریخچه به اینجا مراجعه نمایید. (به زبان انگلیسی)

همچنین ترسیم‌های آنلاین دیگری را در اینجا مشاهده نمایید.

شروع روش اصل موضوعی و مبادی آن به هندسه و کتاب اصول (یا مقدمات) اقلیدس باز می‌گردد. در مقاله زیر ابتدا به‌طور عمده به روش اقلیدس در هندسه پرداخته می‌شود و سپس در علوم دیگر نیز به طور اجمالی، دستگاه‌‌های اصل موضوعی بررسی می‌‌گردند.

روش‌شناسی قیاسی (دستگاه‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌های اصل موضوعی)

نوشته دکتر لطف‌اله نبوی - زمستان ۱۳۶۹ خورشیدی - نشریه مدرس علوم انسانی-  شماره ۲

در پیوند زیر، خلاصه‌ای از آغاز اصول همراه با توضیحات کافی در نشان دادن نارسایی‌های اصول و شکاف در اثبات‌‌های اقلیدس راهنمای بسیار خوبی است.

هندسه اقلیدسی - فارسی
فصل اول کتاب سال استال(S. Stahl)

در پیوند زیر، برخی از انگیزه‌‌های احتمالی اقلیدس از وضع تعاریف، اصول موضوع و مفاهیم متعارف در آغاز کتاب اصول صحبت به میان آمده است و همچنین اصول هیلبرت در هندسه اقلیدسی تبیین شده‌اند.

بنیاد هندسه اقلیدسی - فارسی
فصل اول کتاب ولف(H. Wolfe)

مقاله زیر در مجله پیک ریاضی (جلد دوم- شماره سوم ) پاییز 1366 خورشیدی چاپ گردیده است. این مقاله درباره اولین تعریف اقلیدس در کتاب اصول است. نظر به جالب بودن بحث آن، می‌توانید از پیوندهای زیر متن انگلیسی یا ترجمه فارسی آن را دریافت نمایید.

نقطه به چه بزرگی است؟ (ترجمه فارسی)

 How big is a point? (R. J. Trudeau - 1983)
متن انگلیسی

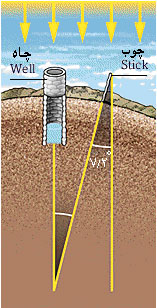
اراتستن در سال 276 قبل ازمیلاد در یونان متولد شد و در سال 194 قبل از میلاد در اسکندریه مصر از دنیا رفت. این دانشمند، رئیس کتابخانه بزرگ اسکندریه نیز بود و  یکی از کارهای مبتکرانه وی، محاسبه شعاع کره زمین با تقریب نزدیک به واقعیت بوده است که در آن زمان به کمک اطلاعات هندسی و با امکانات ناچیز و نادقیق، برای اولین بار در حدود 2200 سال پیش انجام شده است. روش هندسی کار او در عکس زیر نمایان است. 

معرفی بخشی از فعالیت‌های کلاسی درس مبانی هندسه

هر دانشجو فقط یک فعالیت با کیفیت بالا به تنهایی و مجزا با دیگران انجام می‌دهد که فرصت ارائه و تحویل آن به تدریج (نه همۀ دانشجویان باهم) تا تاریخ است. در غیر‌ این‌صورت، در از دانشجویانی که فعالیت نداشته‌اند یا با کیفیت بالا نبوده است،یک آزمون میانی از فصل‌های اول، دوم و سوم و چهارم و پنجمبرگزار می‌گردد. 

- تثلیث زاویۀ دلخواه به کمک سهمی یا هذلولی یا کنکوئید یا یک لیماسیون (جداگانه)

- بیان و اثبات قضیۀ مورلی و دلیل اهمیت آن

- عکس قضیه مورلی و اثبات آن و تعمیم قضیۀ مورلی

- رسم هفت ضلعی منتظم + روش ابن هیثم برای آن با شرح تاریخی

- اثبات حکم پروژۀ یک ص 75 + انجام کامل آن پروژه

- فهرست 23 مسألۀ هیلبرت و معرفی آنها و شرحی تاریخی از حل آنها

- رسم عمودها با خط کش مدرج توسط هیلبرت (پروژۀ 4 ص 124)

- پروژۀ یک ص 158

- تلاش نافرجام خواجه نصیرالدین طوسی برای اثبات اصل توازی و نقایص آن

- چهار ضلعی ساکری و مقایسۀ آن با چهارضلعی خیام + شرح تاریخی

- معرفی اجسام افلاطونی و شرح تاریخی آنها همراه با توضیحات مربوطه

- فعالیت‌های دیگری در آیندۀ نزدیک اضافه می‌شوند.

دانشجوی گرامی، پاسخ این نمونه سؤال‌ها داخل کتاب درسی است. البته با توجه به توضیحات مطلب قبلی سایت، برخی از این سؤال‌ها حذف می‌باشند که تشخیص آنها به عهده دانشجو است.

تذکر مهم:  همچنین خودآزمایی‌هایی فصل‌بندی شده همراه با آدرس پاسخ در متن کتاب، به‌صورت دست‌نویس در مطالب قبلی این سایت آمده است.

نمونه اول 

نمونه دوم

دانشجوی گرامی، آزمون پایانی مبانی هندسه در شرایط ذیل صدق می‌کند:

* مطالب فصل اول به‌طور کامل + خودآزمایی آخر فصل + تمرین تا پایان ص ۳۸

* فصل دوم همه مطالب غیر از بخش صفحه تصویری و آفین تا ص ۶۸ + خودآزمایی آخر فصل + تمرین تا پایان شماره ۱۱ در ص ۷۱

* فصل سوم همه مطالب غیر از ابتدای ص ۱۰۵ تا پایان ص ۱۰۹ + خودآزمایی آخر فصل 

* فصل چهارم همه مطالب غیر از اثبات قضیه ص ۱۴۱ + خودآزمایی آخر فصل

* فصل پنجم به‌طور کامل + خودآزمایی آخر فصل

* فصل ششم از ابتدا تا اول بخش «موازی‌های که عمود مشترک می‌پذیرند» + خودآزمایی آخر فصل در حد مطالب

* فصل هفتم از ص ۲۳۷ تا پایان ص ۲۴۰ + سؤوال ۱ و ۲ خودآزمایی آخر فصل در ص ۲۸۳

* فصل هشتم به‌طور کامل + خودآزمایی آخر فصل

** اثبات قضیه‌هایی که برهان آنها در کتاب درسی نیامده، در آزمون مطرح نمی‌شوند.

**  از داخل مطالب این سایت در آزمون، سؤال متناسب با درس به صورت مقدماتی مطرح می‌شود.

** تعریف‌ها، بُنداشت‌ها و صورت قضیه‌های اسم‌دار کتاب درسی را با دقت مطالعه نمایید.

** مطالب تاریخی و فلسفی کتاب درسی اهمیت به‌سزایی در آزمون دارند.

**  نمونه سؤال به‌زودی در سایت قرار داده می‌شود.

در پیوند زیر، خلاصه‌ای از آغاز اصول همراه با توضیحات کافی در نشان دادن نارسایی‌های اصول و شکاف در اثبات‌‌های اقلیدس راهنمای بسیار خوبی است.

هندسه اقلیدسی - فارسی
فصل اول کتاب سال استال(S. Stahl)

در پیوند زیر، برخی از انگیزه‌‌های احتمالی اقلیدس از وضع تعاریف، اصول موضوع و مفاهیم متعارف در آغاز کتاب اصول صحبت به میان آمده است و همچنین اصول هیلبرت در هندسه اقلیدسی تبیین شده‌اند.

بنیاد هندسه اقلیدسی - فارسی
فصل اول کتاب ولف (H. Wolfe)

هندسه پیش از اقلیدس + درباره کتاب اقلیدس + کشف هندسه نااقلیدسی
فصل اول کتاب «بنیان‌های هندسه» نوشته تین (V. I. Kostin) ترجمه پرویز شهریاری ۱۳۸۱